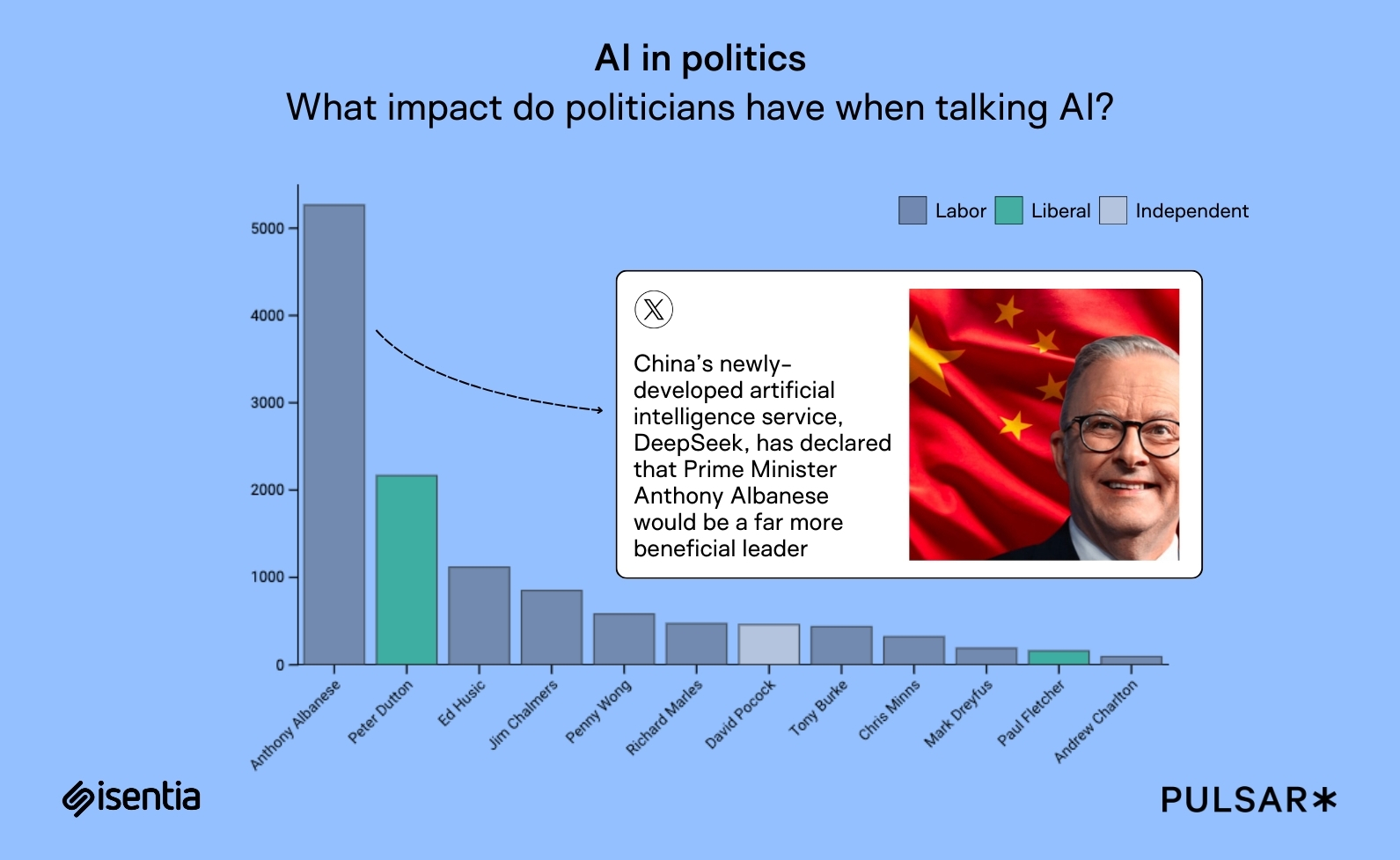
Making optimal decisions without having all the cards in hand

The article “Revelations: A Decidable Class of POMDP with Omega-Regular Objectives” won an Outstanding Paper Award at the AAAI 2025 conference, a prestigious international conference about artificial intelligence. This year, only three papers received such an award out of 3,000 accepted and 12,000 submitted! This recognition crowns the results of research initiated in Bordeaux (France) within the Synthèse team at the Bordeaux Computer Science Research Laboratory (LaBRI), where four of the authors work: Marius Belly, Nathanaël Fijalkow, Hugo Gimbert, and Pierre Vandenhove. The work also involved researchers from Paris (Florian Horn) and Antwerp (Guillermo A. Pérez). The article is freely available on arXiv, and this post outlines its main ideas.

The Synthèse team at LaBRI tackles the challenging problem of program synthesis—developing algorithms that themselves generate other algorithms based on a few examples or a specification of what is expected. In practice, these powerful algorithms are used in various contexts. For example, most spreadsheet applications today offer auto-fill functions: you fill in a few cells, and based on these examples, a small algorithm is synthesized on the fly to complete the rest (DeepSynth). Another example is robotic control: an operator assigns a task to a robot, such as regaining control of the ball in a Robocup match, and the robot’s algorithms determine the right sequence of movements and actions to achieve the goal.

The genesis of this work is a great illustration of our research activity, which is international, interdisciplinary, and collaborative. The award-winning AAAI paper has its roots in a conference held in Maastricht (Netherlands) in 2022, where computer scientists, mathematicians, and economists gathered. At this event, Guillaume Vigeral and Bruno Ziliotto presented their research on the mathematical study of “information revelation” phenomena. The research then unfolded across Europe—from the sunny climate of Bordeaux in the west to Warsaw in the east, invigorated by the Polish weather, passing through Paris, Maastricht, and Antwerp. The results were not achieved in a day but through a process of trials, failures, dead ends, and conjectures of varying solidity, gradually enriched by the perspectives and expertise of different contributors. This is a classic experience in research: when tackling a new problem, one starts with tiny steps. As understanding deepens, those steps grow larger until the problem is solved—or not. Doing research means learning to walk again with every new challenge!

When engineers and AI researchers need to solve synthesis problems, they commonly use a mathematical formalism called Markov Decision Processes, or simply MDP. The central question is: in a situation requiring a sequence of decisions described by an MDP, how can one make good decisions? Or even better—how can one automatically compute the best possible sequence of decisions, also known as an optimal strategy?

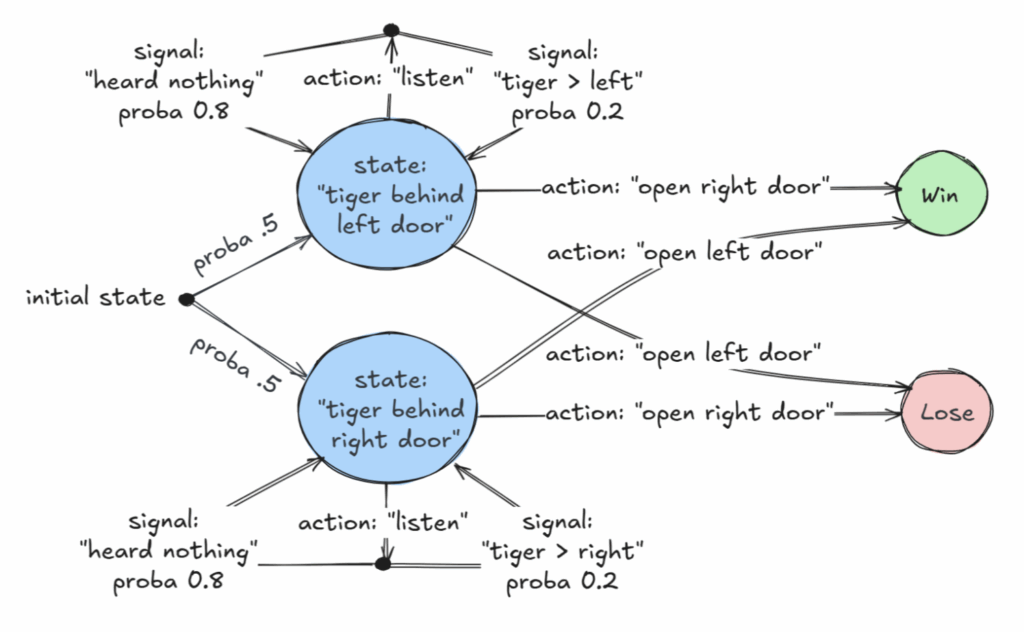
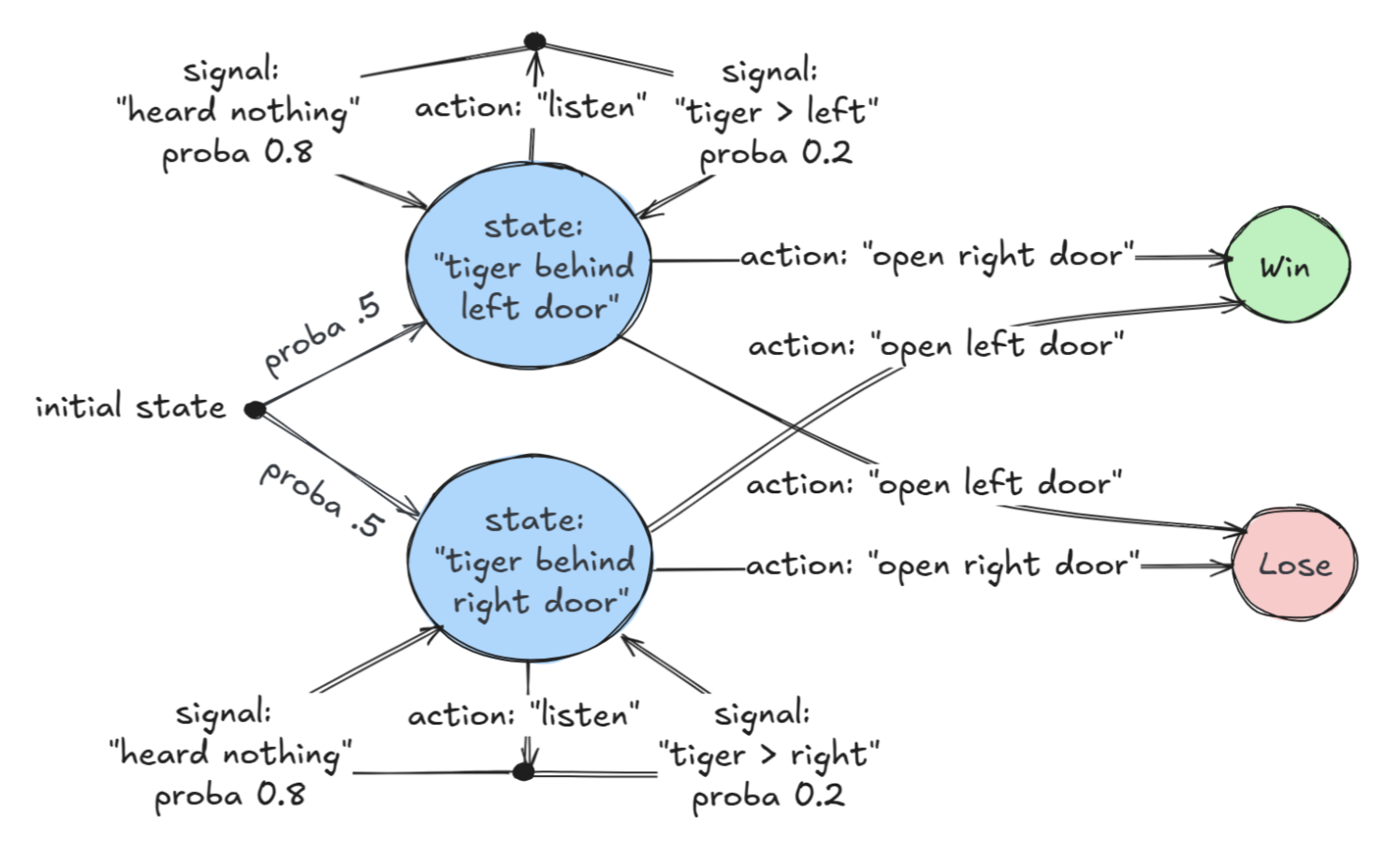
What exactly is an MDP?

In the context of this research, an MDP is a finite-state system whose evolution is determined both by decisions (choosing an action) and by chance. Here is what such a beast looks like:

In everyday life, MDPs can be useful in many situations—for example, when playing Solitaire, also known as Patience or Spider Solitaire in its popular variant. The scenario below demonstrates a decision-making moment in an MDP: should a black king be placed on the empty stack to the left? If so, which one? The decision is challenging because many cards remain face down and will only be revealed later¹.

¹ Even when all the cards are revealed, the problem is not trivial.

Two main types of AI algorithms for solving MDPs

There are two major categories of AI algorithms for solving MDPs, which may seem similar at first but are quite distinct to computer scientists:

1. Heuristic-based algorithms – These work well in practice but lack a theoretical explanation for why they succeed. Most machine learning methods, especially those using neural networks (DeepRL), fall into this category.
2. Exact algorithms – These are guaranteed to always provide the correct answer, but are often slower than heuristic-based algorithms. They belong to the field of trustworthy AI, based on the notions of computability and decidability pioneered by Alan Turing.

Our article falls into the second category: the proposed algorithm reliably computes an exact solution in the form of an optimal strategy, which can be used with complete confidence.

The limits of exact computation and AI learning

Let’s be realistic—DeepRL-based learning techniques can compute strategies for highly complex instances, while exact techniques based on computability theory are currently limited to simpler instances. For instance, Google DeepMind used DeepRL techniques to synthesize outstanding strategies for StarCraft, a popular video game requiring dozens of decisions per second based on millions of parameters. DeepMind’s AI initially defeated the world’s best players, but its strategy was not optimal—unforeseen counter-strategies were later discovered.

Exact methods are currently impractical for solving a problem as complex as StarCraft, but that does not prevent them from being effective in practice. For example, another success story from Bordeaux: the Rhoban team at LaBRI won a gold medal at Robocup 2023 by using exact methods to solve small MDP, relying on information-sharing among multiple cooperative robots.

The complexity of decision problems and the role of information

The difficulty of solving decision problems varies greatly depending on the information available at the time of decision-making. The ideal case is perfect information, where all data is available. A classic example is a robot navigating a maze where the layout and the robot’s exact position and orientation are known. In this case, computing a solution is relatively easy: the algorithm can find a path to the exit (e.g., using Dijkstra’s algorithm) and follow it step by step.

However, in real-world problems, it is rare to have all the information. For example, in Solitaire, some cards are hidden, requiring the player to make assumptions. In general, such problems cannot be solved exactly: according to Turing’s computability theory, no algorithm—no matter how powerful the computer running it—can always solve all MDP control problems with precision. This may seem discouraging, but it doesn’t stop computer scientists from identifying special cases where the problem becomes simpler. In theoretical computer science, these are called decidable classes.

The contribution of the award-winning research

The AAAI-awarded research identifies a decidable class of MDP: decision problems with “strong revelations,” where there is always a nonzero probability that the exact state of the world will be revealed at each step. The paper also provides decidability results for “weak revelations,” where the exact state is guaranteed to be revealed eventually but not necessarily at every step—similar to Solitaire, where hidden cards are gradually uncovered.

A research paper should always look to the future and open new directions. The proposed algorithm can analyze MDPs with revelations (strong ones). An interesting perspective is to reverse the problem: what happens when the algorithm is used in any game, with or without revelations? This could enable the analysis of all games, even the most complex ones, by restricting either the type of strategies players can use or the amount of information they can process.