2429. Minimize XOR

2429. Minimize XOR

Difficulty: Medium

Topics: Greedy, Bit Manipulation

Given two positive integers num1 and num2, find the positive integer x such that:

• x has the same number of set bits as num2, and
• The value x XOR num1 is minimal.

Note that XOR is the bitwise XOR operation.

Return the integer x. The test cases are generated such that x is uniquely determined.

The number of set bits of an integer is the number of 1's in its binary representation.

Example 1:

• Input: num1 = 3, num2 = 5
• Output: 3
• Explanation: The binary representations of num1 and num2 are 0011 and 0101, respectively.
  • The integer 3 has the same number of set bits as num2, and the value 3 XOR 3 = 0 is minimal.

Example 2:

• Input: num1 = 1, num2 = 12
• Output: 3
• Explanation: The binary representations of num1 and num2 are 0001 and 1100, respectively.
  • The integer 3 has the same number of set bits as num2, and the value 3 XOR 1 = 2 is minimal.

Constraints:

• 1 <= num1, num2 <= 109

Hint:

1. To arrive at a small xor, try to turn off some bits from num1
2. If there are still left bits to set, try to set them from the least significant bit

Solution:

The idea is to manipulate the bits of num1 and match the number of set bits (1s) in num2 while minimizing the XOR result. Here's the step-by-step approach:

Steps:

1. Count the Set Bits in num2:

   • Find the number of 1s in the binary representation of num2. Let's call this setBitsCount.

2. Create a Result Number x:

   • Start with x = 0.
   • From the binary representation of num1, preserve the 1s in the most significant positions that match setBitsCount.
   • If there are not enough 1s in num1, add extra 1s starting from the least significant bit.

3. Optimize XOR Result:

   • By aligning the set bits of x with the most significant 1s of num1, the XOR value will be minimized.

4. Return the Result:

   • Return the computed value of x.

Let's implement this solution in PHP: 2429. Minimize XOR

/**
 * @param Integer $num1
 * @param Integer $num2
 * @return Integer
 */
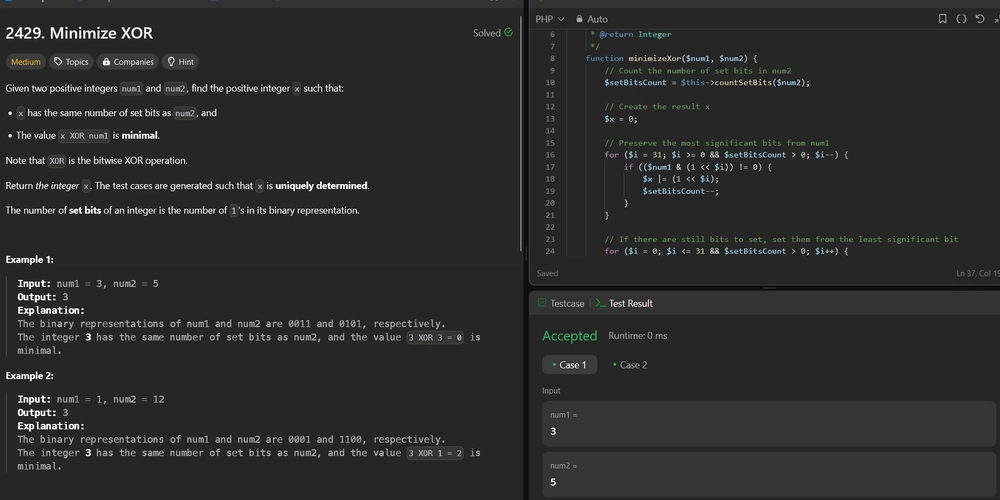
function minimizeXor($num1, $num2) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

/**
 * Helper function to count the number of set bits in a number
 *
 * @param $num
 * @return int
 */
function countSetBits($num) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Test cases
echo minimizeXor(3, 5) . "\n"; // Output: 3
echo minimizeXor(1, 12) . "\n"; // Output: 3
?>

Explanation:

1. countSetBits Function:

   • This function counts the number of 1s in the binary representation of a number using a loop.

2. Building x:

   • First, the most significant 1s from num1 are retained in x to minimize the XOR value.
   • If more 1s are required to match setBitsCount, they are added starting from the least significant bit (to keep the XOR minimal).

3. Optimization:

   • The XOR value is minimized by aligning the significant bits as much as possible between num1 and x.

Complexity:

• Time Complexity: O(32), since the loop iterates a constant number of times (32 bits for integers).
• Space Complexity: O(1), as no extra space is used apart from variables.

Example Walkthrough:

Example 1:

• num1 = 3 (0011) and num2 = 5 (0101).
• setBitsCount = 2.
• x starts as 0.
• From num1, keep two most significant 1s: x = 3 (0011).
• x XOR num1 = 0, which is minimal.

Example 2:

• num1 = 1 (0001) and num2 = 12 (1100).
• setBitsCount = 2.
• From num1, retain 1 and add one more bit to x: x = 3 (0011).
• x XOR num1 = 2, which is minimal.

This ensures the correct and efficient computation of x.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks