Understanding Insertion Sort Algorithm (with Examples in Java)
Insertion sort is a sorting algorithm that works by iteratively inserting each element in an unsorted list into its correct position in a sorted portion of the list. This algorithm is very similar to sorting cards in your hand. We assume that the first card is already sorted, then we take the second card and place it to the right of the sorted card if it is smaller, or to the left if it is bigger. We will continue this process for the remaining cards. Working of Insertion Sort Let's say we want to sort this array in ascending order. First Iteration We assume that the first element is already sorted, so we will start the iteration from the second element. We will compare the element, 2, with the element in the sorted portion of the array, 8. Since 2 is less than 8, we move 8 to the right and 2 to the left. Second Iteration We will compare the current element, 6, with the elements in the sorted portion of the array, 2 and 8. Since 6 is less than 8, we move 8 to the right and 6 to the left. 6 is greater than 2 so it is now in its correct position. This process is repeated until the entire array is sorted. Implementation of Selection Sort public class InsertionSortTest { public static void main(String[] args) { int[] arr = {8, 2, 6, 4, 9, 1}; System.out.println("Unsorted array: " + Arrays.toString(arr)); insertionSort(arr); System.out.println("Sorted array: " + Arrays.toString(arr)); } public static void insertionSort(int[] arr){ // loop through array starting from second element for (int i = 1; i < arr.length; i++) { int key = arr[i]; // set element at i as key // loop backwards through sorted elements to find // where to insert the key element int j = i-1; while (j >= 0 && key < arr[j]) { // move element greater than key to the right arr[j+1] = arr[j]; j--; } arr[j+1] = key; } } } In the code above, we iterate through the array starting from the second element. Inside the first loop, we set the current element as the key, and then we compare it with each element in the sorted portion of the array by looping backward from i-1 until we find its correct position. For example, in the second iteration, when i = 2: We set the current element as the key: In the while block, we iterate backward through the sorted section of the array. In the first iteration of while loop, j = 1 (i-1). If the current element in the sorted section is greater than the key, we move it to the right by saying arr[j+1] = arr[j]: In the second iteration, j = 0. The key 6 is greater than the current element 2, so it does not satisfy the second condition for the while loop and we break out of the while loop. After breaking out of the loop, we insert the key after the element smaller than it by saying arr[j=1] = key. The key is now in its correct position and we can move on to the next iteration. Running the code above will print the following output to the console: Unsorted array: [8, 2, 6, 4, 9, 1] Sorted array: [1, 2, 4, 6, 8, 9] Complexity of Insertion Sort Time Complexity: Best Case (O(n)): The best case is when the array is already sorted. The algorithm performs n−1 comparisons (one for each element except the first) and no shifts. Therefore, the time complexity is O(n). Average Case (O(n²)): This occurs when the array's elements are arranged randomly. For each insertion, every element is compared with all previously inserted elements. Worst Case (O(n²)): The worst case is when the array is sorted in reverse order. Each element must be compared with all previous elements and shifted. Space Complexity O(1): Insertion Sort is an in-place algorithm and requires no additional memory other than a few variables for looping and temporary storage during shifts. Conclusion Insertion Sort has an O(n²) time complexity in the average and worst cases. It is unsuitable when working with large datasets of randomly arranged data due to its high time complexity. Use Insertion Sort when working with small datasets, or when the list is nearly sorted.

Insertion sort is a sorting algorithm that works by iteratively inserting each element in an unsorted list into its correct position in a sorted portion of the list. This algorithm is very similar to sorting cards in your hand. We assume that the first card is already sorted, then we take the second card and place it to the right of the sorted card if it is smaller, or to the left if it is bigger. We will continue this process for the remaining cards.
Working of Insertion Sort
Let's say we want to sort this array in ascending order.
First Iteration
We assume that the first element is already sorted, so we will start the iteration from the second element.
We will compare the element, 2, with the element in the sorted portion of the array, 8. Since 2 is less than 8, we move 8 to the right and 2 to the left.
Second Iteration
We will compare the current element, 6, with the elements in the sorted portion of the array, 2 and 8. Since 6 is less than 8, we move 8 to the right and 6 to the left. 6 is greater than 2 so it is now in its correct position.
This process is repeated until the entire array is sorted.
Implementation of Selection Sort
public class InsertionSortTest {
public static void main(String[] args) {
int[] arr = {8, 2, 6, 4, 9, 1};
System.out.println("Unsorted array: " + Arrays.toString(arr));
insertionSort(arr);
System.out.println("Sorted array: " + Arrays.toString(arr));
}
public static void insertionSort(int[] arr){
// loop through array starting from second element
for (int i = 1; i < arr.length; i++) {
int key = arr[i]; // set element at i as key
// loop backwards through sorted elements to find
// where to insert the key element
int j = i-1;
while (j >= 0 && key < arr[j]) {
// move element greater than key to the right
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
}
}
In the code above, we iterate through the array starting from the second element. Inside the first loop, we set the current element as the key, and then we compare it with each element in the sorted portion of the array by looping backward from i-1 until we find its correct position.
For example, in the second iteration, when i = 2:
We set the current element as the key:
In the while block, we iterate backward through the sorted section of the array. In the first iteration of while loop, j = 1 (i-1). If the current element in the sorted section is greater than the key, we move it to the right by saying arr[j+1] = arr[j]:
In the second iteration, j = 0. The key 6 is greater than the current element 2, so it does not satisfy the second condition for the while loop and we break out of the while loop.
After breaking out of the loop, we insert the key after the element smaller than it by saying arr[j=1] = key.
The key is now in its correct position and we can move on to the next iteration.
Running the code above will print the following output to the console:
Unsorted array: [8, 2, 6, 4, 9, 1]
Sorted array: [1, 2, 4, 6, 8, 9]
Complexity of Insertion Sort
Time Complexity:
Best Case (O(n)):
The best case is when the array is already sorted. The algorithm performs n−1 comparisons (one for each element except the first) and no shifts. Therefore, the time complexity is O(n).
Average Case (O(n²)):
This occurs when the array's elements are arranged randomly. For each insertion, every element is compared with all previously inserted elements.
Worst Case (O(n²)):
The worst case is when the array is sorted in reverse order. Each element must be compared with all previous elements and shifted.
Space Complexity O(1):
Insertion Sort is an in-place algorithm and requires no additional memory other than a few variables for looping and temporary storage during shifts.
Conclusion
Insertion Sort has an O(n²) time complexity in the average and worst cases. It is unsuitable when working with large datasets of randomly arranged data due to its high time complexity. Use Insertion Sort when working with small datasets, or when the list is nearly sorted.

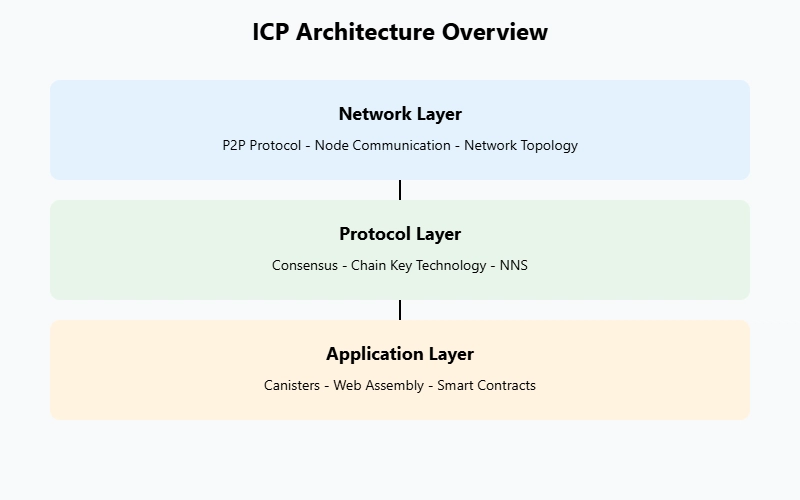








_marcos_alvarado_Alamy.jpg?#)