Modelling data relationships with F# types
An F# example implementation of Ghosts of Departed Proofs. In a previous article, Encapsulating rod-cutting, I used a code example to discuss how to communicate an API's contract to client developers; that is, users of the API. In the article, I wrote "All this said, however, it's also possible that I'm missing an obvious design alternative. If you can think of a way to model this relationship in a non-predicative way, please write a comment." And indeed, a reader helpfully offered an alternative: "Regarding the relation between the array and the index, you will find the paper called "Ghosts of departed proofs" interesting. Maybe an overkill in this case, maybe not, but a very interesting and useful technique in general." borar I wouldn't call it 'an obvious design alternative', but nonetheless find it interesting. In this article, I'll pick up the code from Encapsulating rod-cutting and show how the 'Ghosts of Departed Proofs' (GDP) technique may be applied. Problem review # Before we start with the GDP technique, a brief review of the problem is in order. For the complete overview, you should read the Encapsulating rod-cutting article. In the present article, however, we'll focus on one particular problem related to encapsulation: Ideally, the cut function should take two input arguments. The first argument, p, is an array or list of prices. The second argument, n, is the size of a rod to cut optimally. One precondition states that n must be less than or equal to the length of p. This is because the algorithm needs to look up the price of a rod of size n, and it can't do that if n is greater than the length of p. The implied relationship is that p is indexed by rod size, so that if you want to find the price of a rod of size n, you look at the nth element in p. How may we model such a relationship in a way that protects the precondition? An obvious choice, particularly in object-oriented design, is to use a Guard Clause. In the F# code base, it might look like this: let cut (p : _ array) n = if p.Length
An F# example implementation of Ghosts of Departed Proofs.
In a previous article, Encapsulating rod-cutting, I used a code example to discuss how to communicate an API's contract to client developers; that is, users of the API. In the article, I wrote
"All this said, however, it's also possible that I'm missing an obvious design alternative. If you can think of a way to model this relationship in a non-predicative way, please write a comment."
And indeed, a reader helpfully offered an alternative:
"Regarding the relation between the array and the index, you will find the paper called "Ghosts of departed proofs" interesting. Maybe an overkill in this case, maybe not, but a very interesting and useful technique in general."
I wouldn't call it 'an obvious design alternative', but nonetheless find it interesting. In this article, I'll pick up the code from Encapsulating rod-cutting and show how the 'Ghosts of Departed Proofs' (GDP) technique may be applied.
Problem review #
Before we start with the GDP technique, a brief review of the problem is in order. For the complete overview, you should read the Encapsulating rod-cutting article. In the present article, however, we'll focus on one particular problem related to encapsulation:
Ideally, the cut function should take two input arguments. The first argument, p, is an array or list of prices. The second argument, n, is the size of a rod to cut optimally. One precondition states that n must be less than or equal to the length of p. This is because the algorithm needs to look up the price of a rod of size n, and it can't do that if n is greater than the length of p. The implied relationship is that p is indexed by rod size, so that if you want to find the price of a rod of size n, you look at the nth element in p.
How may we model such a relationship in a way that protects the precondition?
An obvious choice, particularly in object-oriented design, is to use a Guard Clause. In the F# code base, it might look like this:
let cut (p : _ array) n = if p.Length <= n then raise (ArgumentOutOfRangeException "n must be less than the length of p") // The rest of the function body...
You might argue that in F# and other functional programming languages, throwing exceptions isn't idiomatic. Instead, you ought to return Result or Option values, here the latter:
let cut (p : _ array) n = if p.Length <= n then None else // The rest of the function body...
To be clear, in most code bases, this is exactly what I would do. What follows is rather exotic, and hardly suitable for all use cases.
Proofs as values #
It's not too hard to model the lower boundary of the n parameter. As is often the case, it turns out that the number must be a natural number. I already covered that in the previous article. It's much harder, however, to model the upper boundary of the value, because it depends on the size of p.
The following is based on the paper Ghosts of Departed Proofs, as well as a helpful Gist also provided by Borar. (The link to the paper is to what I believe is the 'official' page for it, and since it's part of the ACM digital library, it's behind a paywall. Even so, as is the case with most academic papers, it's easy enough to find a PDF of it somewhere else. Not that I endorse content piracy, but it's my impression that academic papers are usually disseminated by the authors themselves.)
The idea is to enable a library to issue a 'proof' about a certain condition. In the example I'm going to use here, the proof is that a certain number is in the valid range for a given list of prices.
We actually can't entirely escape the need for a run-time check, but we do gain two other benefits. The first is that we're now using the type system to communicate a relationship that otherwise would have to be described in written documentation. The second is that once the proof has been issued, there's no need to perform additional run-time checks.
This can help move an API towards a more total, as opposed to partial, definition, which again moves towards what Michael Feathers calls unconditional code. This is particularly useful if the alternative is an API that 'forgets' which run-time guarantees have already been checked. The paper has some examples. I've also recently encountered similar situations when doing Advent of Code 2024. Many days my solution involved immutable maps (like hash tables) that I'd recurse over. In many cases I'd write an algorithm where I with absolute certainty knew that a particular key was in the map (if, for example, I'd just put it there three lines earlier). In such cases, you don't want a total function that returns an option or Maybe value. You want a partial function. Or a type-level guarantee that the value is, indeed, in the map.
For the example in this article, it's overkill, so you may wonder what the point is. On the other hand, a simple example makes it easier to follow what's going on. Hopefully, once you understand the technique, you can extrapolate it to situations where it might be more warranted.
Proof contexts #
The overall idea should look familiar to practitioners of statically-typed functional programming. Instead of plain functions and data structures, we introduce a special 'context' in which we have to run our computations. This is similar to how the IO monad works, or, in fact, most monads. You're not supposed to get the value out of the monad. Rather, you should inject the desired behaviour into the monad.
We find a similar design with existential types, or with the ST monad, on which the ideas in the GDP paper are acknowledged to be based. We even see a mutation-based variation in the article A mutable priority collection, where we may think of the Edit API as a variation of the ST monad, since it allows 'localized' state mutation.
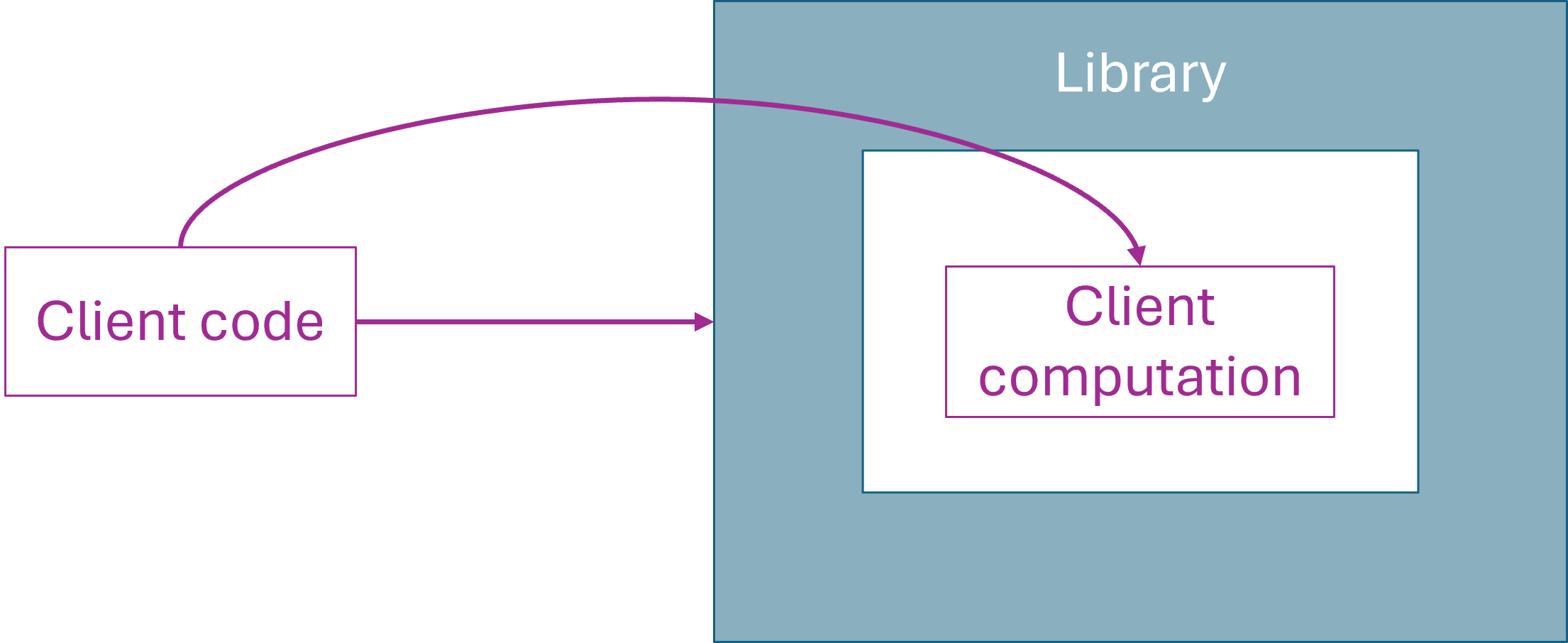
I'll attempt to illustrate it like this:

A library offers a set of functions and data structures for immediate use. In addition, it also provides a higher-oder function that enables client code to embed a computation into a special 'sandbox' area where special rules apply. The paper calls such a context a 'name', which it does because it's trying to be as general as possible. As I'm writing this, I find it easier to think of this 'sandbox' as a 'proof context'. It's a context in which proof values exist. Crucially, as we shall see, they don't exist outside of this context.
Size proofs #
In the rod-cutting example, we particularly care about proving that a given number n is within the size of the price list. We do this by representing the proof as a value:
type Size<'a> = private Size of int with member this.Value = let (Size i) = this in i override this.ToString () = let (Size i) = this in string i
Two things are special about this type definition:
- The constructor is
private. - It has a phantom type
'a.
A phantom type is a generic type parameter that has no run-time value. Notice that Size<'a> contains no value of the type 'a. The type only exists at compile-time.
You can think of the type parameter as similar to a security token. The issuer of the proof associates a particular security token to vouch for its validity. Usually, when we talk about security tokens, they do have a run-time representation (typically a byte array) because we need to exchange them with other processes. This is, for example, how claims-based authentication works.

In this case, our concern isn't security. Rather, we wish to communicate and enforce certain relationships. Since we wish to leverage the type system, we use a type as a token.

Since the Size constructor is private, the library controls how it issues proofs, a bit like a claims issuer can sign a claim with its private key.
Okay, but how are Size proofs issued?
Issuing size proofs #
As you'll see later, more than one API may issue Size proofs, but the most fundamental is that you can query a price list for such a proof:
type PriceList<'a> = private PriceList of int list with member this.Length = let (PriceList prices) = this in prices.Length member this.trySize candidate : Size<'a> option = if 0 < candidate && candidate <= this.Length then Some (Size candidate) else None
The trySize member function issues a Some Size<'a> value if the candidate is within the size of the price array. As discussed above, we can't completely avoid a run-time check, but now that we have the proof, we don't need to repeat that run-time check if we wanted to use a particular Size value with the same PriceList.
Notice how immutability is an essential part of this design. If, in the object-oriented manner, we allow a price list to change, we could make it shorter. This could invalidate some proof that we previously issued. Since, however, the price list is immutable, we can trust that once we've checked a size, it remains valid. You can also think of this as a sort of encapsulation, in the sense that once we've assured ourselves that an object, or here rather a value, is valid, it remains valid. Indeed, encapsulation is simpler with immutability.
You probably still have some questions. For instance, how do we ensure that a size proof issued by one price list can't be used against another price list? Imagine that you have two price lists. One has ten prices, the other twenty. You could have the larger one issue a proof that size 17 is valid. What prevents you from using that proof with the smaller price list?
That's the job of that phantom type. Notice how a PriceList<'a> issues a Size<'a> proof. It's the same generic type argument.
Usually, I extol F#'s type inference. I prefer not having to use type annotations unless I have to. When it comes to GDP, however, type annotations are necessary, because we need these phantom types to line up. Without the type annotations, they wouldn't do that.
In the above example, the smaller price list might have the type PriceList<'a> and the larger one the type PriceList<'b>. The smaller would issue proofs of the type Size<'a>, and the larger one proofs of the type Size<'b>. As you'll see, you can't use a Size<'a> where a Size<'b> is required, or vice versa.
You may still wonder how one then creates PriceList<'a> values. After all, that type also has a private constructor.
We'll get back to that later.
Proof-based cut API #
Before we look at how client code may consume APIs based on proofs such as Size<'a>, we should review their expressive power. What does this design enable us to say?
While the first example above, with the Guard Clause alternative, was based on the initial imperative implementation shown in the article Implementing rod-cutting, the rest of the present article builds on the refactored code from Encapsulating rod-cutting.
The first change I need to introduce is to the Cut record type:
type Cut<'a> = { Revenue : int; Size : Size<'a> }
Notice that I've changed the type of the Size property to Size<'a>. This has the implication that Cut<'a> now also has a phantom type, and since client code can't create Size<'a> values, by transitivity it means that neither can client code create Cut<'a> values. These values can only be issued as proofs.
This enables us to change the type definition of the cut function:
let cut (PriceList prices : PriceList<'a>) (Size n : Size<'a>) : Cut<'a> list = // Implementation follows here...
Notice how all the phantom types line up. In order to call the function, client code must supply a Size<'a> value issued by a compatible PriceList<'a> value. Upon a valid call, the function returns a list of Cut<'a> values.
Pay attention to what is being communicated. You may find this strange and impenetrable, but for a reader who understands GDP, much about the contract is communicated through the types. We can see that n relates to prices, because the 'proof token' (the generic type parameter 'a) is the same for both arguments. A reader who understands how Size<'a> proofs are issued will now understand what the preconditions is: The n argument must be valid according to the size of the prices argument.
The type of the cut function also communicates a postcondition: It guarantees that the Size values of each Cut<'a> returned is valid according to the supplied prices. In other words, it means that no defensive coding is necessary. Client code doesn't have to check whether or not the price of each indicated cut can actually be found in prices. The types guarantee that they can.
You may consider the cut function a 'secondary' issuer of Size<'a> proofs, since it returns such values. If you wanted to call cut again with one of those values, you could.
Compared to the previous article, I don't think I changed much else in the cut function, besides the initial function declaration, and the last line of code, but for good measure, here's the entire function:
let cut (PriceList prices : PriceList<'a>) (Size n : Size<'a>) : Cut<'a> list = // Implementation follows here... let p = 0 :: prices |> Array.ofList let findBestCut revenues j = [1..j] |> List.map (fun i -> p[i] + Map.find (j - i) revenues, i) |> List.maxBy fst let aggregate acc j = let revenues = snd acc let q, i = findBestCut revenues j let cuts = fst acc cuts << (cons (q, i)), Map.add revenues.Count q revenues [1..n] |> List.fold aggregate (id, Map.add 0 0 Map.empty) |> fst <| [] // Evaluate Hughes list |> List.map (fun (r, i) -> { Revenue = r; Size = Size i })
The cut function is part of the same module as Size<'a>, so even though the constructor is private, the cut function can still use it.
Thus, the entire proof mechanism is for external use. Internally, the library code may take shortcuts, so it's up to the library author to convince him- or herself that the contract holds. In this case, I'm quite confident that the function only issues valid proofs. After all, I've lifted the algorithm from an acclaimed text book, and this particular implementation is covered by more than 10,000 test cases.
Proof-based solve API #
The solve code hasn't changed, I believe:
let solve prices n = let cuts = cut prices n let rec imp n = if n <= 0 then [] else let idx = n - 1 let s = cuts[idx].Size s :: imp (n - s.Value) imp n.Value
While the code hasn't changed, the type has. In this case, no explicit type annotations are necessary, because the types are already correctly inferred from the use of cut:
solve: prices: PriceList<'a> -> n: Size<'a> -> Size<'a> list
Again, the phantom types line up as desired.
Proof-based revenue calculation #
Although I didn't show it in the previous article, I also included a function to calculate the revenue from a list of cuts. It gets the same treatment as the other functions:
let calculateRevenue (PriceList prices : PriceList<'a>) (cuts : Size<'a> list) = cuts |> List.sumBy (fun s -> prices[s.Value - 1])
Again we see how the GDP-based API communicates a precondition: The cuts must be valid according to the prices; that is, each cut, indicated by its Size property, must be guaranteed to be within the range defined by the price list. This makes the function total; or, unconditional code, as Michael Feathers would put it. The function can't fail at run time.
(I am, once more, deliberately ignoring the entirely independent problem of potential integer overflows.)
While you could repeatedly call PriceList<'a>.trySize to produce a list of cuts, the most natural way to produce such a list of cuts is to first call cut, and then pass its result to calculateRevenue.
The function returns int.
Proof-based printing #
Finally, here's printSolution:
let printSolution p n = solve p n |> List.iter (printfn "%O")
It hasn't changed much since the previous incarnation, but the type is now PriceList<'a> -> Size<'a> -> unit. Again, the precondition is the same as for cut.
Running client code #
How in the world do you write client code against this API? After all, the types all have private constructors, so we can't create any values.
If you trace the code dependencies, you'll notice that PriceList<'a> sits at the heart of the API. If you have a PriceList<'a>, you'd be able to produce the other values, too.
So how do you create a PriceList<'a> value?
You don't. You call the following runPrices function, and give it a PriceListRunner that it'll embed and run in the 'sandbox' illustrated above.
type PriceListRunner<'r> = abstract Run<'a> : PriceList<'a> -> 'r let runPrices pl (ctx : PriceListRunner<'r>) = ctx.Run (PriceList pl)
As the paper describes, the GDP trick hinges on rank-2 polymorphism, and the only way (that I know of) this is supported in F# is on methods. An object is therefore required, and we define the abstract PriceListRunner<'r> class for that purpose.
Client code must implement the abstract class to call the runPrices function. Fortunately, since F# has object expressions, client code might look like this:
[<Fact>] let ``CLRS example`` () = let p = [1; 5; 8; 9; 10; 17; 17; 20; 24; 30] let actual = Rod.runPrices p { new PriceListRunner<_> with member __.Run pl = option { let! n = pl.trySize 10 let cuts = Rod.cut pl n return List.map (fun c -> (c.Revenue, c.Size.Value)) cuts } } [ ( 1, 1) ( 5, 2) ( 8, 3) (10, 2) (13, 2) (17, 6) (18, 1) (22, 2) (25, 3) (30, 10) ] |> Some =! actual
This is an xUnit.net test where actual is produced by runPrices and an object expression that defines the code to run in the proof context. When the Run method runs, it runs with a concrete type that the compiler picked for 'a. This type is only in scope within that method, and can't escape it.
The implementing class is given a PriceList<'a> as an input argument. In this example, it tries to create a size of 10, which succeeds because the price list has ten elements.
Notice that the Run method transforms the cuts to tuples. Why doesn't it return cuts directly?
It can't. It's part of the deal. If I change the last line of Run to return cuts, the code no longer compiles. The compiler error is:
This code is not sufficiently generic. The type variable 'a could not be generalized because it would escape its scope.
Remember I wrote that 'a can't escape the scope of Run? This is enforced by the type system.
Preventing misalignment #
You may already consider it a benefit that this kind of API design uses the type system to communicate pre- and postconditions. Perhaps you also wonder how it prevents errors. As already discussed, if you're dealing with multiple price lists, it shouldn't be possible to use a size proof issued by one, with another. Let's see how that might look. We'll start with a correctly coded unit test:
[<Fact>] let ``Nest two solutions`` () = let p1 = [1; 2; 2] let p2 = [1] let actual = Rod.runPrices p1 { new PriceListRunner<_> with member __.Run pl1 = option { let! n1 = pl1.trySize 3 let cuts1 = Rod.solve pl1 n1 let r = Rod.calculateRevenue pl1 cuts1 let! inner = Rod.runPrices p2 { new PriceListRunner<_> with member __.Run pl2 = option { let! n2 = pl2.trySize 1 let cuts2 = Rod.solve pl2 n2 return Rod.calculateRevenue pl2 cuts2 } } return (r, inner) } } Some (3, 1) =! actual
This code compiles because I haven't mixed up the Size or Cut values. What happens if I 'accidentally' change the 'inner' Rod.solve call to let cuts2 = Rod.solve pl2 n1?
The code doesn't compile:
Type mismatch. Expecting a 'Size<'a>' but given a 'Size<'b>' The type ''a' does not match the type ''b'
This is fortunate, because n1 wouldn't work with pl2. Consider that n1 contains the number 3, which is valid for the larger list pl1, but not the shorter list pl2.
Proofs are issued with a particular generic type argument - the type-level 'token', if you will. It's possible for a library API to explicitly propagate such proofs; you see a hint of that in cut, which not only takes as input a Size<'a> value, but also issues new proofs as a result.
At the same time, this design prevents proofs from being mixed up. Each set of proofs belongs to a particular proof context.
You get the same compiler error if you accidentally mix up some of the other terms.
Conclusion #
One goal in the GDP paper is to introduce a type-safe API design that's also ergonomic. Matt Noonan, the author, defines ergonomic as a design where correct use of the API doesn't place an undue burden on the client developer. The paper's example language is Haskell where rank-2 polymorphism has a low impact on the user.
F# only supports rank-2 polymorphism in method definitions, which makes consuming a GDP API more awkward than in Haskell. The need to create a new type, and the few lines of boilerplate that entails, is a drawback.
Even so, the GDP trick is a nice addition to your functional tool belt. You'll hardly need it every day, but I personally like having some specialized tools lying around together with the everyday ones.
But wait! The reason that F# has support for rank-2 polymorphism through object methods is because C# has that language feature. This must mean that the GDP technique works in C# as well, doesn't it? Indeed it does.
Next: Modelling data relationships with C# types.
This blog is totally free, but if you like it, please consider supporting it.
What's Your Reaction?




























