Using Optimization to Solve Adversarial Problems

An example of simultaneously optimizing two policies for two adversarial agents, looking specifically at the cat and mouse game.

In the previous article on optimization, I looked at finding an optimal strategy for the Betting on the World Series problem. In this article, I look at a more difficult problem, developing a policy for two adversarial players in a board game.

I look specifically at the cat and mouse game, where we have two players, the cat and mouse, placed on an n x m grid, similar to a chess board, but where it is possible to have any number of rows and any number of columns. Either the cat or mouse may move first, and they then take turns until there is a winner. At each step, they must move either left, right, up, or down; they cannot remain in the same cell, and cannot move diagonally. So, they generally have four possible moves, though if at an edge will have only three, and if in a corner, only two.

The cat wins if it’s able to capture the mouse, which is achieved by moving to the same cell the mouse is on. The mouse wins by evading capture for sufficiently long. We’ll look at a couple of ways to define that.

Each starts in opposite corners, with the cat in the bottom-left, and the mouse in the top-right, so at the beginning (if we have 8 rows and 7 columns), the board looks like:

There are a number of approaches to training the cat and the mouse to play well at this game. At a high level, we can group these into two main types of approach: 1) where the players each determine their moves as they play; and 2) where the players each determine, prior to play, a complete policy related to how they’ll move in each situation.

The first type of approach is what’s more generally used with games and is usually more scalable and robust, at least with more complex games. For this problem, though, as it’s relatively straightforward, I’ll look at methods to learn a complete, deterministic policy for each player, which they can simply execute during play.

Determining each move during play

So, while determining a complete policy ahead of time is feasible for the cat and mouse game, this is not the case more more complex games. With an application trained to play, for example, chess, it cannot feasibly develop a policy ahead of time that could indicate how to handle every situation it may encounter during a game; chess is far too complex to allow this.

In future articles, I’ll look at techniques to allow players to assess their current situation each step, and move based on their evaluations during play. For here, though, I’ll just provide a very quick overview of techniques to determine the moves to make during play.

There are different ways to develop, for example, a chess-playing application, but the traditional method is to construct what’s called a game tree. As well, reinforcement learning is often used to develop game-playing applications, and a combination can also be used.

A game tree describes each possible sequence of moves each player can make, starting at the current board. For example, in chess, it may be black’s turn and black may have, say, 8 legal moves. The root node of the game tree will represent the current board. The boards that result from black’s current possible moves are the next level of the tree, so the 2nd level of the tree will have 8 possible boards. For each of these, white has some set of legal moves. If the 8 boards in the 2nd layer each have, say, 10 legal responses from white, then there are 80 boards at the 3rd level. The 4th level is then the boards the result from all the possible moves black could make given the boards in the 3rd level, and so on. In this way, each layer of the tree is many times larger than the previous layer.

For simple games like tic-tac-toe or Connect 4, it’s possible to create the full game tree and determine definitively the best move at each step. For more complex games such as checkers, chess, go, and so on, this isn’t possible. Instead, though, we may build the game trees out for only a finite number of steps, and estimate the quality of the board for the current player at each leaf node.

So, if the tree extends, say, five levels deep, we will have set of boards on the fifth level of the tree, but few of these will be a win for either player. We must, though, assess if the board is better for one player or the other. For checkers or chess and similar games, this can be done by simply counting the pieces. A more effective, but slower, method is to also look at the board position. For example, with chess we can evaluate how advanced each piece is, how exposed, and so on.

It’s also possible to use what’s called Monte Carlo Tree Search. Here the tree leaves are expanded by playing each board out to completion, but through a set of some number of random games (where both player play entirely randomly). This is a means of evaluating each board, but without analyzing the board itself. So, it a tree is built out to 5 layers, there may be 1000 boards at that level. To evaluate each of these, we can perform some fixed number of random games starting from each of these boards and count how often each player wins, which gives a decent estimate of how strong the board is for both players.

Policy-based solutions for the cat and mouse game

The cat and mouse game is fairly straight-forward, and developing a single fully-defined policy for the cat, and another for the mouse, (allowing both to simply follow this in a deterministic manner during play) is actually feasible. This is particularly true with the first case we look at, where we assume the board is a known, fixed size, and where this is relatively small. We look at the more difficult case, where the board size is very large, later.

In the image here, there’s a very small, 3x3 board. It’s fairly easy to see in this case that the cat could develop a fully-defined policy, specifying what it would do when it is in any one of the 9 squares and the mouse is in any one of the 9 squares. Taking every combination of where the cat may be and the mouse may be, there are only 81 combinations, and it’s possible to train a policy to play optimally in each of these 81 scenarios. That is, in the case of the cat’s policy, in each of the 81 cases, we have a direction (either left, right, up, or down) that the cat will move, and similarly for the mouse’s policy.

Optimal play in the cat and mouse game

Depending on the size and shape of the board and which player goes first, with perfect play (where neither player makes a mistake), there is actually a known winner for the cat and mouse game.

To picture this, consider the case of a 3x3 board. Similar to tic-tac-toe, it’s possible for the cat (and similarly for the mouse) to create a game tree covering every move it can make, every response the mouse can make, every next move for the cat, and so on for as many moves as it takes until the game is over (either the cat captures the mouse, or the mouse evades capture for sufficiently long). Doing this, given that a game has a finite and relatively small length, it’s possible to consider every possible sequence of moves, and determine the ideal move in each possible scenario.

However, we also want to support much larger boards, for example 8 x 8 boards, where considering every possible sequence of moves may be infeasible. Here, the game trees may grow to enormous sizes. So, as indicated above, developing partial games trees and then assessing the boards in the leaf nodes would be quite possible. But, developing a complete game trees is not feasible.

In these case, though, it’s still possible to develop a full policy for both players using a Hill-Climbing optimization technique. In an example below, we do this for a 8x7 board. Here there are 56 square on the board, so 56 places the cat may be and 56 places the mouse may be (actually 55 given that if they’re on the same square, the game is over and the cat has already won, but we’ll simplify this by assuming each player may be on any square).

There are then 3,136 possible combinations of their locations, and so developing a policy for play for each player (at least when using the first, and simplest, method I’ll describe here — where each player has a defined move, either left, right, up, or down, for each combination of cat and mouse position) requires developing a policy of size 3,136.

This will not scale up to much larger boards (we’ll cover a similar method, that does cover arbitrarily large boards later), but does cover moderate sized boards well, and is a good place to begin.

When does the cat win?

Before we look at an algorithmic solution to this problem, the cat and mouse game is an interesting problem in itself, and may be good to stop here for a bit and think about: when is the game winnable for the cat, and when is it not (so that the mouse is able to win)? I’ll give you a little time to think about that before going over the answer.

. . .

Thinking…

. . .

Thinking some more…

. . .

Don’t look until you’re ready to see the answer…

. . .

Okay, I’ll go over at least one way to look at this. Like a lot of similar problems, this can be viewed in terms of the colours on a chess board. The squares alternate between black and white. Each move, the mouse moves from one colour to the other and the mouse does as well.

Both players start on a certain colour of square. Let’s say the cat (in the bottom-left) is on a black square. If there are an even number of rows and an even number of columns (as with an 8 x 8 chess board), the square where the mouse starts (in the top-right) will also be black.

If the cat plays first, it moves from a black square to a white. The mouse will then as well. So after each time the cat and the mouse move, they will both be on the same colour (both on black, or both on white). Which means, when the cat moves, it is moving to a square of the opposite colour as what the mouse is currently on. The cat can never catch the mouse.

In this case, there’s actually no winnable policy for the mouse per se: it can just move randomly, so long as it does not move into the cat (essentially, a suicidal move). But, the cat does require a good policy (or it will not be able to capture the mouse before an allowed number of moves), and moving randomly will not likely result in a win (though interestingly can quite often with a sufficiently small board).

For the mouse, though there is no winnable strategy in this case, there is still a sense of optimal play — that it avoids capture for at least as long as is possible.

If the number of rows or columns is odd, or if the mouse moves first, on the other hand, the cat can capture the mouse. To do this, it just needs to approach the mouse so that it is diagonally next to the mouse, which will force the mouse away from the cat, in one of two possible directions, depending specifically how they are situated. The cat can then follow the mouse, remaining diagonally next to the mouse until it is eventually forced into a corner and captured.

In this case, the mouse cannot win when the cat is playing optimally, but can still win where the cat is not, as it just has to avoid capture for some defined number of moves.

The next image has an example where the cat has moved diagonally next to the mouse, forcing the mouse towards one of the corners (in this case, the top-right corner).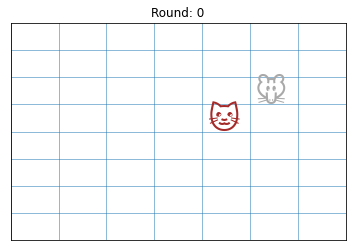

Once the mouse is in a corner (as shown below), if the cat is diagonally next to the mouse, the mouse will lose the next move. It will have only two legal moves, both to squares adjacent to the cat, where the cat can move onto the mouse its next move.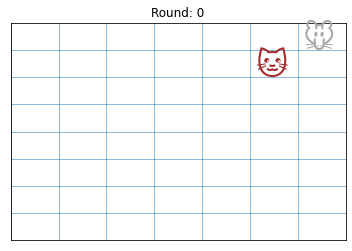

Training two separate strategies

The question, then, is how to train the two players, starting from no knowledge, to play a perfect game, meaning both players play optimally and neither makes a mistake.

We can consider two cases:

1. Where the game is winnable for the cat. In this case, we want to ensure we can train a cat to reliably win, regardless of how the mouse plays. This means learning to move close to the mouse, and to corner it. And, we wish to ensure the mouse evades capture for as long as possible.
2. Where the game is unwinnable for the cat. In this case, we want to ensure that we’ve trained the mouse well enough to evade capture for long enough be declared the winner. And, we want to ensure the cat is trained well enough that it can capture the mouse if the mouse does make a mistake.

Clearly the cat and mouse game is far simpler than games like chess, checker, Go, or Othello, but it does have one difficulty, which is that the game is asymmetric, and the two players must each develop separate strategies.

With games where there is only one strategy required, it’s possible to let two players play against each other, and develop progressively better strategies over time. This is the approach we’re going to take here as well, but, similar to what’s often done when training a Generative Adversarial Network, the code actually alternates between training the cat, and training the mouse. That is, it trains the cat until it is able to win, then the mouse until it’s able to win, then the cat, and so on.

Approaches to Determining an optimal policy

As the goal is to develop an optimal policy, it’s fairly natural to use an optimization technique, which we do here. Some choices for this include hill climbing, simulated annealing, genetic algorithms, and swarm intelligence algorithms.

Each have their merits, but for this article, as with the Betting on the World Series article, we’ll look at hill-climbing approaches to develop a policy for both players. Hill climbing is likely the simplest of the optimization techniques just listed, but is sufficient to handle this problem. In future articles I’ll cover more difficult problems and more involved solutions to these.

Hill climbing, for either player in a game such as this, starts with some policy (often created randomly, or initialized to something somewhat reasonable), and then gradually improves, through a process of repeatedly trying small variations, selecting the best of these, trying small variations to that, and so on until eventually what looks like an optimal solution is reached.

Using a small, fixed board size

As indicated, in the first approach we look at, we develop a policy in likely the simplest manner we can: the cat’s policy specifies the specific move to make given each combination of the cat’s location and the mouse’s location. Similarly for the mouse’s policy.

For an 8x7 board, this requires a policy of size 3,136 for each player. Initially, the policy will be set to be very poor: in this example, we specify for both players to simply always move up, unless on the top row, in which case, they move down. But, over time, the hill climbing process moves towards increasingly strong policies for both players.

The code related to this article is hosted on github, in the CatAndMouseGame repository. What we’re considering now is in the version_1 notebook.

The first cell contains some options, which you can adjust to see how the training proceeds with different values.

NUM_ROWS = 8
NUM_COLS = 7

FIRST_MOVE = "cat"           # Set to "cat" or "mouse"
INITIAL_CAT_POLICY = "WEAK"  # Set to "WEAK" or "STRONG"
ANIMATION_TIME_PER_MOVE = 0.5

For brevity, I won’t cover the INITIAL_CAT_POLICY for this, and will assume it’s set to ‘weak’, but if set to ‘strong’, the cat will be initialized to always move towards the mouse (if set to ‘weak’, it must learn this).

The code starts with initializing the board, so that the two players are in opposite corners. It also initializes the policies for both players (as described above — so both player always move up unless on the top row, in which case they move down).

It then plays one game. As the games are deterministic, it requires only one game to determine the winner for a given cat policy and given mouse policy. The results of this first game are the baseline the cat then tries to repeatedly improve on until it’s able to beat the mouse. We then repeatedly improve the mouse until it’s able to be the cat, and so on.

This is set to execute for 100,000 iterations, which executes in a few minutes, and is enough to establish quite good play for both players.

Evaluating each game

As the cat learns, it has, at any point in time, the current policy: the best policy discovered so far. It then creates a number of variations on this, each with a small number of modifications to this current-best policy (changing the direction moved by the cat in a small number of the 3,126 cells of the policy). It then evaluates each of these by playing against the current-best policy for the mouse. The cat then takes the best-performing of these candidate new policies (unless none improve over the current best policy for the cat, in which case it continues generating random variations until at least one is discovered that improves over this.)

For Hill climbing to work well, it needs to be able to detect even small improvements from one policy to the next. So, it would be difficult to implement this if the player knew only, after each game, if they won or not.

Instead, after each game, we report the number of moves until there was a winner, and the distance the two players were apart at the end of the game. When the cat wins, this will be zero. Where the mouse wins, though, the cat wants to minimize this: it wants to end at least close to the mouse. And the mouse wants to maximize this: it wants to end far from the cat.

In general, for the cat, an improvement is found if the previous-best resulted in a win for the mouse and a new policy results in a win for the cat. But, also, if the mouse won in the previous best, and the mouse still wins, but the cat ends in a position closer to the mouse. Or, if the cat won in the previous best and still wins, but does so in fewer moves.

Interestingly, it’s also useful here to reward longer games for the cat, at least to an extent. This encourages the cat to move around more, and to not stay in the same area. We do have to be careful though, as we do not wish to encourage the cat to proceed slower than necessary when it is able to capture the mouse.

For the mouse, an improvement is found if the previous-best resulted in a win for the cat and a new policy results in a win for the mouse. As well, there is an improvement if the cat won with the previous best and the cat still wins, but the game is longer. And there is an improvement if the mouse won in the previous best and the mouse still does, but ends further from the cat.

Code for Version 1

The full code is provided here, as well as on github.

In each iteration, either the cat is learning or the mouse is learning, where learning here means trying new policies and selecting the best of these.

def init_board():
    # The cat starts in the bottom-left corner; the mouse in the upper-right.
    # The y values start with 0 at the bottom, with the top row being NUM_ROWS-1
    board = {'cat_x': 0, 
             'cat_y': 0, 
             'mouse_x': NUM_COLS-1, 
             'mouse_y': NUM_ROWS-1}
    return board

def draw_board(board, round_idx):
    clear_output(wait=True)
    s = sns.scatterplot(x=[], y=[])
    for i in range(NUM_ROWS):
        s.axhline(i, linewidth=0.5)
    for i in range(NUM_COLS):
        s.axvline(i, linewidth=0.5)    
    s.set_xlim(0, NUM_COLS)
    s.set_ylim(0, NUM_ROWS)
    offset = 0.1 
    size = 250 / max(NUM_ROWS, NUM_COLS)
    plt.text(board['cat_x'] + offset, board['cat_y'] + offset, '