TELL: Explaining neural networks using logic
Alexa Steinbrück / Better Images of AI / Explainable AI / Licenced by CC-BY 4.0 Would you trust an artificial intelligence software to make a diagnosis for you? Most people would answer negatively to this question. Indeed, despite the significant advancements of AI and neural networks, their ”black box” nature is a significant barrier to […]
 Alexa Steinbrück / Better Images of AI / Explainable AI / Licenced by CC-BY 4.0
Alexa Steinbrück / Better Images of AI / Explainable AI / Licenced by CC-BY 4.0
Would you trust an artificial intelligence software to make a diagnosis for you? Most people would answer negatively to this question. Indeed, despite the significant advancements of AI and neural networks, their ”black box” nature is a significant barrier to our trust. The inability to understand how or why a model arrives at its conclusions leaves many skeptical about its use, particularly in sensitive areas like healthcare, finance, or legal systems. This is where Explainable AI (XAI) comes into play, a research area focused on interpreting AI models’ predictions.
Our paper contributes to this field by developing a novel neural network that can be directly transformed into logic. Why logic? From an early age, we are taught to reason using logical statements. Logic forms the backbone of how humans explain decisions, make sense of complex problems, and communicate reasoning to others. By embedding logic into the structure of a neural network, we aim to make its predictions interpretable in a way that feels intuitive and trustworthy to people.
Previous works like Logic Explained Networks (Ciravegna et al., 2023) proposed providing explanations in the form of logic by using truth tables. Although this approach provides a good balance between retaining the power of neural networks and having explanations for their predictions, their explanation generation is done post-hoc. This means that explanations are derived after the model is trained by identifying logical relationships between the output and the input. Consequently, the generated logical explanations may not perfectly align with the model’s behavior.
In our paper, we propose to address this issue by developing a novel neural network layer called the Transparent Explainable Logic Layer, or TELL. This layer allows us to derive rules directly from the model’s weights, ensuring alignment between the model’s predictions and the rules.
TELL
Among the first examples that are usually shown in deep learning classes, we often find architectures that are capable of approximating logic gates. It is exactly from these architectures that we got the inspiration for a layer that could represent logic rules. For instance, if we examine the AND and OR gates represented in Figure 1, we can observe that by using the Heaviside step function, it is possible to exploit the bias to threshold input values and thereby replicate the behavior of these gates.
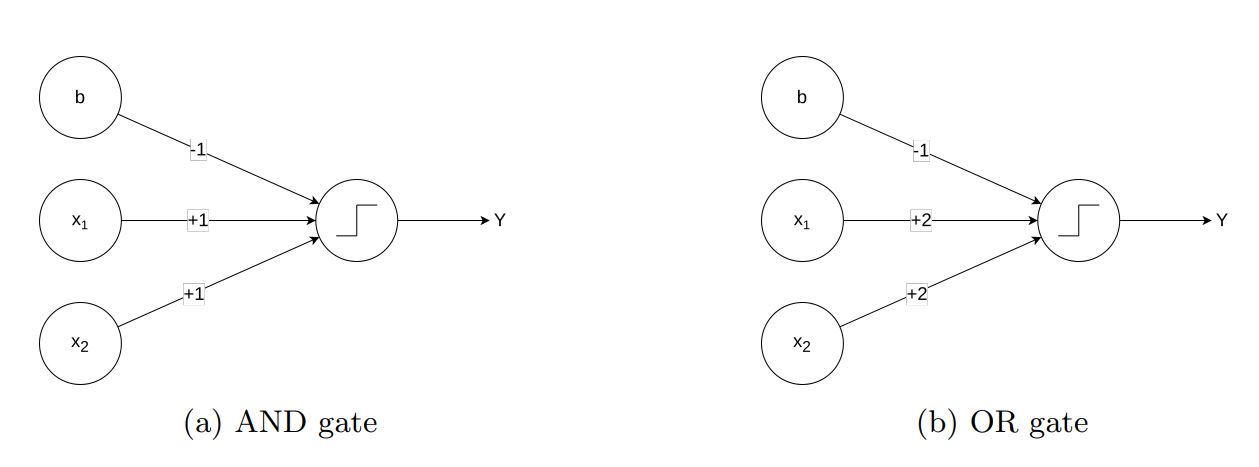 Figure 1: Graphical representation of two neural network architectures that approximate the AND and OR logic gates
Figure 1: Graphical representation of two neural network architectures that approximate the AND and OR logic gates
While these architectures provide a compelling demonstration of how neural networks can emulate logic gates, defining architectures that can learn logic rules is far from straightforward. Specifically, the Heaviside step function used in these examples poses significant challenges to training via gradient descent. The intuition behind TELL lies in replacing the Heaviside function with the sigmoid function, which can approximate its behavior while allowing for gradient-based optimization. Consider a linear layer with the sigmoid activation function:
![]() .
.
We know that to yield a positive outcome, the argument of the sigmoid must be positive. This means that if we can find all the sets of weights such that the argument is positive, we could completely explain our layer. However, as the number of features increases, finding these combinations becomes computationally complex. To simplify this, we assume binary inputs and positive weights (while allowing the bias to take any value). Formally, this assumption ensures the layer is “monotonic”, meaning that increasing the value of any feature either maintains or increases the layer’s output. Assuming binary inputs, each feature acts as a ”switch” that toggles a specific weight on or off. By identifying all input combinations that produce a positive sum, we can derive the layer’s logic rules.
For clarity, let’s take this example where ![]() :
:
![]() .
.
It is easy to see that, given an input ![]() , the argument of the sigmoid adds up to
, the argument of the sigmoid adds up to ![]() , which is positive, then yielding a positive outcome. On the contrary, considering an input
, which is positive, then yielding a positive outcome. On the contrary, considering an input ![]() the argument of the sigmoid adds up to
the argument of the sigmoid adds up to ![]() , that yield a negative outcome as the argument sums up to a negative value.
, that yield a negative outcome as the argument sums up to a negative value.
Now, it is clearer how we can obtain logic rules from the layer: we simply need to identify the subsets of features with corresponding weights that sum up to a value that is greater than ![]() . To do so, we can start from the highest weight and try all the combinations of weights, adding them in decreasing order. For the example above, for instance, the resulting explanation would be:
. To do so, we can start from the highest weight and try all the combinations of weights, adding them in decreasing order. For the example above, for instance, the resulting explanation would be:
![]() .
.
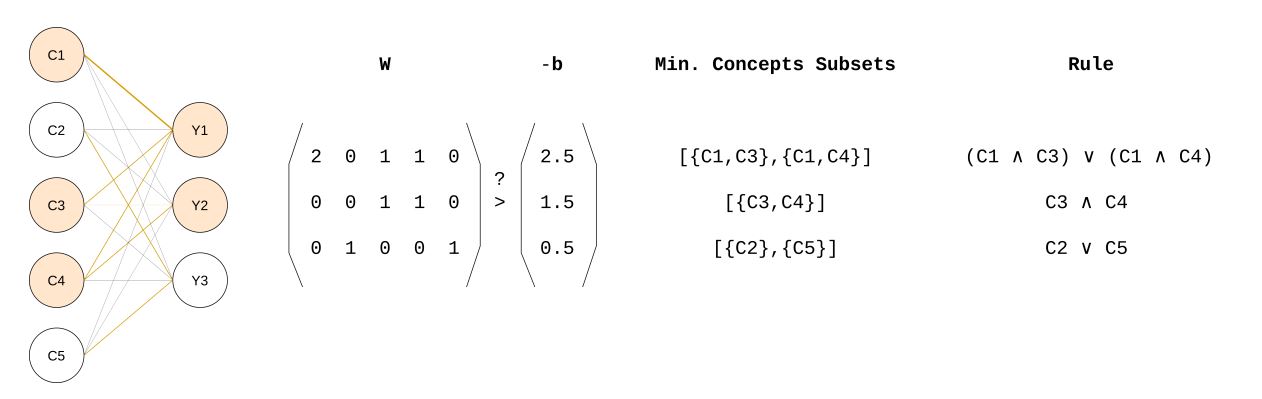 Figure 2: Architecture of TELL in the case of multi-output. For each output, we extract the subsets of weights that sum up to a value greater than
Figure 2: Architecture of TELL in the case of multi-output. For each output, we extract the subsets of weights that sum up to a value greater than ![]() , and we report the corresponding logical rules.
, and we report the corresponding logical rules.
Figure 2 proposes a visual scheme of the procedure just explained in the case of multiple outputs. For space and reading fluidity, in this post, we do not go into the details of the mathematical proof and implementation of the layer, but you can find them in the published article. Now that we have defined how we can design a layer that is readable into logic rules, in the next section, we can look at the algorithm that allows us to retrieve these rules from a trained model. The rule extraction procedure
consists of a recursive function over the weights that searches for all the subsets with a sum above the negative of the bias. The naïve approach iterates over all the combinations of weights. Thanks to the monotonic property of TELL, in practice, we do not have to look for all the combinations of the weights. In fact, before starting the search, we sort the weights in descending order. Here is a Python implementation for the rule extraction procedure:
 Listing 1: Python function to find logic rules
Listing 1: Python function to find logic rules
Overall, TELL provides a novel approach to embedding logical reasoning directly into neural networks, ensuring that explanations align naturally with the model’s behavior. This work represents a step forward in making AI systems more transparent and trustworthy, especially for sensitive applications. For further details, here is a list of useful resources the reader could use:
- Our Paper: Transparent Explainable Logic Layers, A. Ragno, M. Plantevit, C. Robardet, R. Capobianco.. ECAI 2024, IOS Press, 2024.
- TELL Repository
- Logic explained networks, G. Ciravegna, P. Barbiero, F. Giannini, M. Gori, P. Lio, M. Maggini, and S. Melacci.. Artificial Intelligence, 2023.



















