Implementing rod-cutting
From pseudocode to implementation in three languages. This article picks up where Implementation and usage mindsets left off, examining how easy it is to implement an algorithm in three different programming languages. As an example, I'll use the bottom-up rod-cutting algorithm from Introduction to Algorithms. Rod-cutting # The problem is simple: "Serling Enterprises buys long steel rods and cuts them into shorter rods, which it then sells. Each cut is free. The management of Serling Enterprises wants to know the best way to cut up the rods." Introduction to Algorithms. Fourth edition, ch. 14.1 You're given an array of prices, or rather revenues, that each size is worth. The example from the book is given as a table: length i 1 2 3 4 5 6 7 8 9 10 price pi 1 5 8 9 10 17 17 20 24 30 Notice that while this implies an array like [1, 5, 8, 9, 10, 17, 17, 20, 24, 30], the array is understood to be one-indexed, as is the most common case in the book. Most languages, including all three languages in this article, have zero-indexed arrays, but it turns out that we can get around the issue by adding a leading zero to the array: [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]. Thus, given that price array, the best you can do with a rod of length 10 is to leave it uncut, yielding a revenue of 30. On the other hand, if you have a rod of length 7, you can cut it into two rods of lengths 1 and 6. Another solution for a rod of length 7 is to cut it into three rods of sizes 2, 2, and 3. Both solutions yield a total revenue of 18. Thus, while more than one optimal solution exists, the algorithm given here only identifies one of them. Extended-Bottom-Up-Cut-Rod(p, n) 1 let r[0:n] and s[1:n] be new arrays 2 r[0] = 0 3 for j = 1 to n // for increasing rod length j 4 q = -∞ 5 for i = 1 to j // i is the position of the first cut 6 if q < p[i] + r[j - i] 7 q = p[i] + r[j - i] 8 s[j] = i // best cut location so far for length j 9 r[j] = q // remember the solution value for length j 10 return r and s Which programming language is this? It's no particular language, but rather pseudocode. The reason that the function is called Extended-Bottom-Up-Cut-Rod is that the book pedagogically goes through a few other algorithms before arriving at this one. Going forward, I don't intend to keep that rather verbose name, but instead just call the function cut_rod, cutRod, or Rod.cut. The p parameter is a one-indexed price (or revenue) array, as explained above, and n is a rod size (e.g. 10 or 7, reflecting the above examples). Given the above price array and n = 10, the algorithm returns two arrays, r for maximum possible revenue for a given cut, and s for the size of the maximizing cut. i 0 1 2 3 4 5 6 7 8 9 10 r[i] 0 1 5 8 10 13 17 18 22 25 30 s[i] 1 2 3 2 2 6 1 2 3 10 Such output doesn't really give a solution, but rather the raw data to find a solution. For example, for n = 10 (= i), you consult the table for (one-indexed) index 10, and see that you can get the revenue 30 from making a cut at position 10 (which effectively means no cut). For n = 7, you consult the table for index 7 and observe that you can get the total revenue 18 by making a cut at position 1. This leaves you with two rods, and you again consult the table. For n = 1, you can get the revenue 1 by making a cut at position 1; i.e. no further cut. For n = 7 - 1 = 6 you consult the table and observe that you ca
From pseudocode to implementation in three languages.
This article picks up where Implementation and usage mindsets left off, examining how easy it is to implement an algorithm in three different programming languages.
As an example, I'll use the bottom-up rod-cutting algorithm from Introduction to Algorithms.
Rod-cutting #
The problem is simple:
"Serling Enterprises buys long steel rods and cuts them into shorter rods, which it then sells. Each cut is free. The management of Serling Enterprises wants to know the best way to cut up the rods."
You're given an array of prices, or rather revenues, that each size is worth. The example from the book is given as a table:
| length i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| price pi | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
Notice that while this implies an array like [1, 5, 8, 9, 10, 17, 17, 20, 24, 30], the array is understood to be one-indexed, as is the most common case in the book. Most languages, including all three languages in this article, have zero-indexed arrays, but it turns out that we can get around the issue by adding a leading zero to the array: [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30].
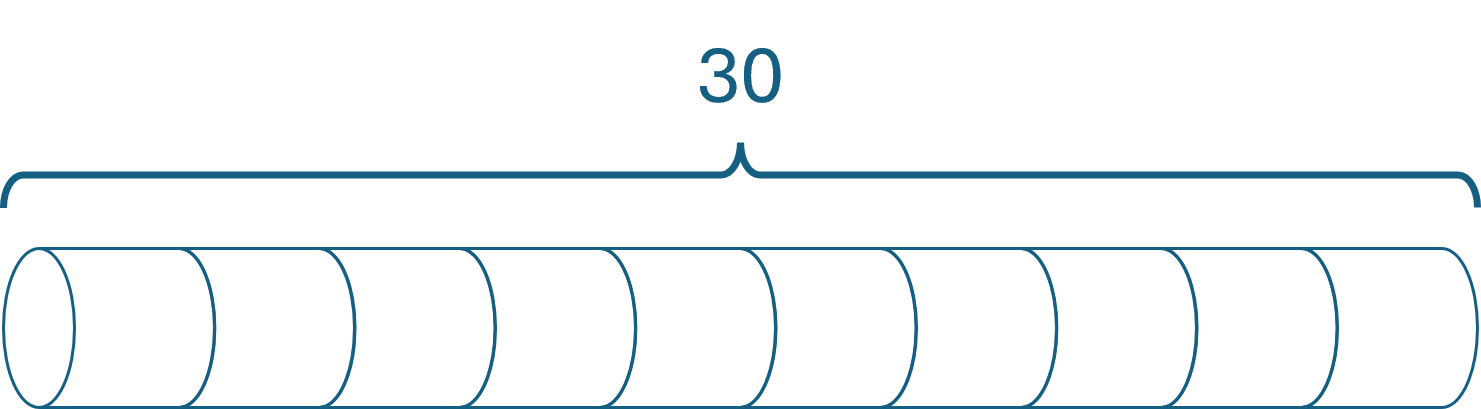
Thus, given that price array, the best you can do with a rod of length 10 is to leave it uncut, yielding a revenue of 30.

On the other hand, if you have a rod of length 7, you can cut it into two rods of lengths 1 and 6.
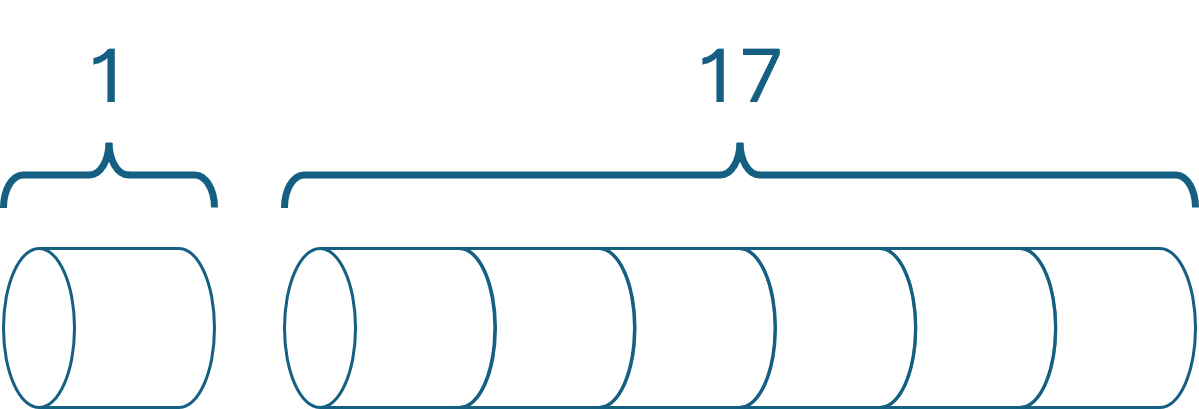
Another solution for a rod of length 7 is to cut it into three rods of sizes 2, 2, and 3. Both solutions yield a total revenue of 18. Thus, while more than one optimal solution exists, the algorithm given here only identifies one of them.
Extended-Bottom-Up-Cut-Rod(p, n) 1 let r[0:n] and s[1:n] be new arrays 2 r[0] = 0 3 for j = 1 to n // for increasing rod length j 4 q = -∞ 5 for i = 1 to j // i is the position of the first cut 6 if q < p[i] + r[j - i] 7 q = p[i] + r[j - i] 8 s[j] = i // best cut location so far for length j 9 r[j] = q // remember the solution value for length j 10 return r and s
Which programming language is this? It's no particular language, but rather pseudocode.
The reason that the function is called Extended-Bottom-Up-Cut-Rod is that the book pedagogically goes through a few other algorithms before arriving at this one. Going forward, I don't intend to keep that rather verbose name, but instead just call the function cut_rod, cutRod, or Rod.cut.
The p parameter is a one-indexed price (or revenue) array, as explained above, and n is a rod size (e.g. 10 or 7, reflecting the above examples).
Given the above price array and n = 10, the algorithm returns two arrays, r for maximum possible revenue for a given cut, and s for the size of the maximizing cut.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| r[i] | 0 | 1 | 5 | 8 | 10 | 13 | 17 | 18 | 22 | 25 | 30 |
| s[i] | 1 | 2 | 3 | 2 | 2 | 6 | 1 | 2 | 3 | 10 |
Such output doesn't really give a solution, but rather the raw data to find a solution. For example, for n = 10 (= i), you consult the table for (one-indexed) index 10, and see that you can get the revenue 30 from making a cut at position 10 (which effectively means no cut). For n = 7, you consult the table for index 7 and observe that you can get the total revenue 18 by making a cut at position 1. This leaves you with two rods, and you again consult the table. For n = 1, you can get the revenue 1 by making a cut at position 1; i.e. no further cut. For n = 7 - 1 = 6 you consult the table and observe that you can get the revenue 17 by making a cut at position 6, again indicating that no further cut is necessary.
Another procedure prints the solution, using the above process:
Print-Cut-Rod-Solution(p, n) 1 (r, s) = Extended-Bottom-Up-Cut-Rod(p, n) 2 while n > 0 3 print s[n] // cut location for length n 4 n = n - s[n] // length of the remainder of the rod
Again, the procedure is given as pseudocode.
How easy is it translate this algorithm into code in a real programming language? Not surprisingly, this depends on the language.
Translation to Python #
The hypothesis of the previous article is that dynamically typed languages may be more suited for implementation tasks. The dynamically typed language that I know best is Python, so let's try that.
def cut_rod(p, n): r = [0] * (n + 1) s = [0] * (n + 1) r[0] = 0 for j in range(1, n + 1): q = float('-inf') for i in range(1, j + 1): if q < p[i] + r[j - i]: q = p[i] + r[j - i] s[j] = i r[j] = q return r, s
That does, indeed, turn out to be straightforward. I had to figure out the syntax for initializing arrays, and how to represent negative infinity, but a combination of GitHub Copilot and a few web searches quickly cleared that up.
The same is true for the Print-Cut-Rod-Solution procedure.
def print_cut_rod_solution(p, n): r, s = cut_rod(p, n) while n > 0: print(s[n]) n = n - s[n]
Apart from minor syntactical differences, the pseudocode translates directly to Python.
So far, the hypothesis seems to hold. This particular dynamically typed language, at least, easily implements that particular algorithm. If we must speculate about underlying reasons, we may argue that a dynamically typed language is low on ceremony. You don't have to get side-tracked by declaring types of parameters, variables, or return values.
That, at least, is a common complaint about statically typed languages that I hear when I discuss with lovers of dynamically typed languages.
Let us, then, try to implement the rod-cutting algorithm in a statically typed language.
Translation to Java #
Together with other C-based languages, Java is infamous for requiring a high amount of ceremony to get anything done. How easy is it to translate the rod-cutting pseudocode to Java? Not surprisingly, it turns out that one has to jump through a few more hoops.
First, of course, one has to set up a code base and choose a build system. I'm not well-versed in Java development, but here I (more or less) arbitrarily chose gradle. When you're new to an ecosystem, this can be a significant barrier, but I know from decades of C# programming that tooling alleviates much of that pain. Still, a single .py file this isn't.
Apart from that, the biggest hurdle turned out to be that, as far as I can tell, Java doesn't have native tuple support. Thus, in order to return two arrays, I would have to either pick a reusable package that implements tuples, or define a custom class for that purpose. Object-oriented programmers often argue that tuples represent poor design, since a tuple doesn't really communicate the role or intent of each element. Given that the rod-cutting algorithm returns two integer arrays, I'd be inclined to agree. You can't even tell them apart based on their types. For that reason, I chose to define a class to hold the result of the algorithm.
public class RodCuttingSolution { private int[] revenues; private int[] sizes; public RodCuttingSolution(int[] revenues, int[] sizes) { this.revenues = revenues; this.sizes = sizes; } public int[] getRevenues() { return revenues; } public int[] getSizes() { return sizes; } }
Armed with this return type, the rest of the translation went smoothly.
public static RodCuttingSolution cutRod(int[] p, int n) { var r = new int[n + 1]; var s = new int[n + 1]; r[0] = 0; for (int j = 1; j <= n; j++) { var q = Integer.MIN_VALUE; for (int i = 1; i <= j; i++) { if (q < p[i] + r[j - i]) { q = p[i] + r[j - i]; s[j] = i; } } r[j] = q; } return new RodCuttingSolution(r, s); }
Granted, there's a bit more ceremony involved compared to the Python code, since one must declare the types of both input parameters and method return type. You also have to declare the type of the arrays when initializing them, and you could argue that the for loop syntax is more complicated than Python's for ... in range ... syntax. One may also complain that all the brackets and parentheses makes it harder to read the code.
While I'm used to such C-like code, I'm not immune to such criticism. I actually do find the Python code more readable.
Translating the Print-Cut-Rod-Solution pseudocode is a bit easier:
public static void printCutRodSolution(int[] p, int n) { var result = cutRod(p, n); while (n > 0) { System.out.println(result.getSizes()[n]); n = n - result.getSizes()[n]; } }
The overall structure of the code remains intact, but again we're burdened with extra ceremony. We have to declare input and output types, and call that awkward getSizes method to retrieve the array of cut sizes.
It's possible that my Java isn't perfectly idiomatic. After all, although I've read many books with Java examples over the years, I rarely write Java code. Additionally, you may argue that static methods exhibit a code smell like Feature Envy. I might agree, but the purpose of the current example is to examine how easy or difficult it is to implement a particular algorithm in various languages. Now that we have an implementation in Java, we might wish to refactor to a more object-oriented design, but that's outside the scope of this article.
Given that the rod-cutting algorithm isn't the most complex algorithm that exists, we may jump to the conclusion that Java isn't that bad compared to Python. Consider, however, how the extra ceremony on display here impacts your work if you have to implement a larger algorithm, or if you need to iterate to find an algorithm on your own.
To be clear, C# would require a similar amount of ceremony, and I don't even want to think about doing this in C.
All that said, it'd be irresponsible to extrapolate from only a few examples. You'd need both more languages and more problems before it even seems reasonable to draw any conclusions. I don't, however, intend the present example to constitute a full argument. Rather, it's an illustration of an idea that I haven't pulled out of thin air.
One of the points of Zone of Ceremony is that the degree of awkwardness isn't necessarily correlated to whether types are dynamically or statically defined. While I'm sure that I miss lots of points made by 'dynamists', this is a point that I often feel is missed by that camp. One language that exemplifies that 'beyond-ceremony' zone is F#.
Translation to F# #
If I'm right, we should be able to translate the rod-cutting pseudocode to F# with approximately the same amount of trouble than when translating to Python. How do we fare?
let cut (p : _ array) n = let r = Array.zeroCreate (n + 1) let s = Array.zeroCreate (n + 1) r[0] <- 0 for j = 1 to n do let mutable q = Int32.MinValue for i = 1 to j do if q < p[i] + r[j - i] then q <- p[i] + r[j - i] s[j] <- i r[j] <- q r, s
Fairly well, as it turns out, although we do have to annotate p by indicating that it's an array. Still, the underscore in front of the array keyword indicates that we're happy to let the compiler infer the type of array (which is int array).
(We can get around that issue by writing Array.item i p instead of p[i], but that's verbose in a different way.)
Had we chosen to instead implement the algorithm based on an input list or map, we wouldn't have needed the type hint. One could therefore argue that the reason that the hint is even required is because arrays aren't the most idiomatic data structure for a functional language like F#.
Otherwise, I don't find that this translation was much harder than translating to Python, and I personally prefer for j = 1 to n do over for j in range(1, n + 1):.
We also need to add the mutable keyword to allow q to change during the loop. You could argue that this is another example of additional ceremony, While I agree, it's not much related to static versus dynamic typing, but more to how values are immutable by default in F#. If I recall correctly, JavaScript similarly distinguishes between let, var, and const.
Translating Print-Cut-Rod-Solution requires, again due to values being immutable by default, a bit more effort than Python, but not much:
let printSolution p n = let _, s = cut p n let mutable n = n while n > 0 do printfn "%i" s[n] n <- n - s[n]
I had to shadow the n parameter with a mutable variable to stay as close to the pseudocode as possible. Again, one may argue that the overall problem here isn't the static type system, but that programming based on mutation isn't idiomatic for F# (or other functional programming languages). As you'll see in the next article, a more idiomatic implementation is even simpler than this one.
Notice, however, that the printSolution action requires no type declarations or annotations.
Let's see it all in use:
> let p = [|0; 1; 5; 8; 9; 10; 17; 17; 20; 24; 30|];; val p: int array = [|0; 1; 5; 8; 9; 10; 17; 17; 20; 24; 30|] > Rod.printSolution p 7;; 1 6
This little interactive session reproduces the example illustrated in the beginning of this article, when given the price array from the book and a rod of size 7, the solution printed indicates cuts at positions 1 and 6.
I find it telling that the translation to F# is on par with the translation to Python, even though the structure of the pseudocode is quite imperative.
Conclusion #
You could, perhaps, say that if your mindset is predominantly imperative, implementing an algorithm using Python is likely easier than both F# or Java. If, on the other hand, you're mostly in an implementation mindset, but not strongly attached to whether the implementation should be imperative, object-oriented, or functional, I'd offer the conjecture that a language like F# is as implementation-friendly as a language like Python.
If, on the other hand, you're more focused on encapsulating and documenting how an existing API works, perhaps that shift of perspective suggests another evaluation of dynamically versus statically typed languages.
In any case, the F# code shown here is hardly idiomatic, so it might be illuminating to see what happens if we refactor it.
Next: Encapsulating rod-cutting.
This blog is totally free, but if you like it, please consider supporting it.




















